Maths
Mathematics at Langdon Park School is designed to unlock potential, foster logical thinking, and equip every student with the quantitative skills essential for success in modern life.
At KS3, our mathematics curriculum builds firm foundations in number, algebra, geometry, ratio, proportion and statistics. Pupils develop fluency in core skills while also learning to reason mathematically and solve problems in different contexts, through a blend of direct instruction, collaborative problem-solving, and investigative tasks. We place emphasis on pupils being able to explain their thinking clearly, helping them build resilience and confidence as they prepare for the challenges of GCSE.
At KS4, pupils continue to extend and deepen their mathematical knowledge. The GCSE curriculum allows them to apply maths to increasingly complex problems, strengthening their ability to make connections across different topics. Alongside preparation for examinations, our aim is to show pupils the value of mathematics in real life, whether that be interpreting data in Science, working with algorithms in Computing, or analysing patterns and trends in Geography and History. These cross-curricular links highlight how mathematics is a vital tool across the curriculum and beyond the classroom.
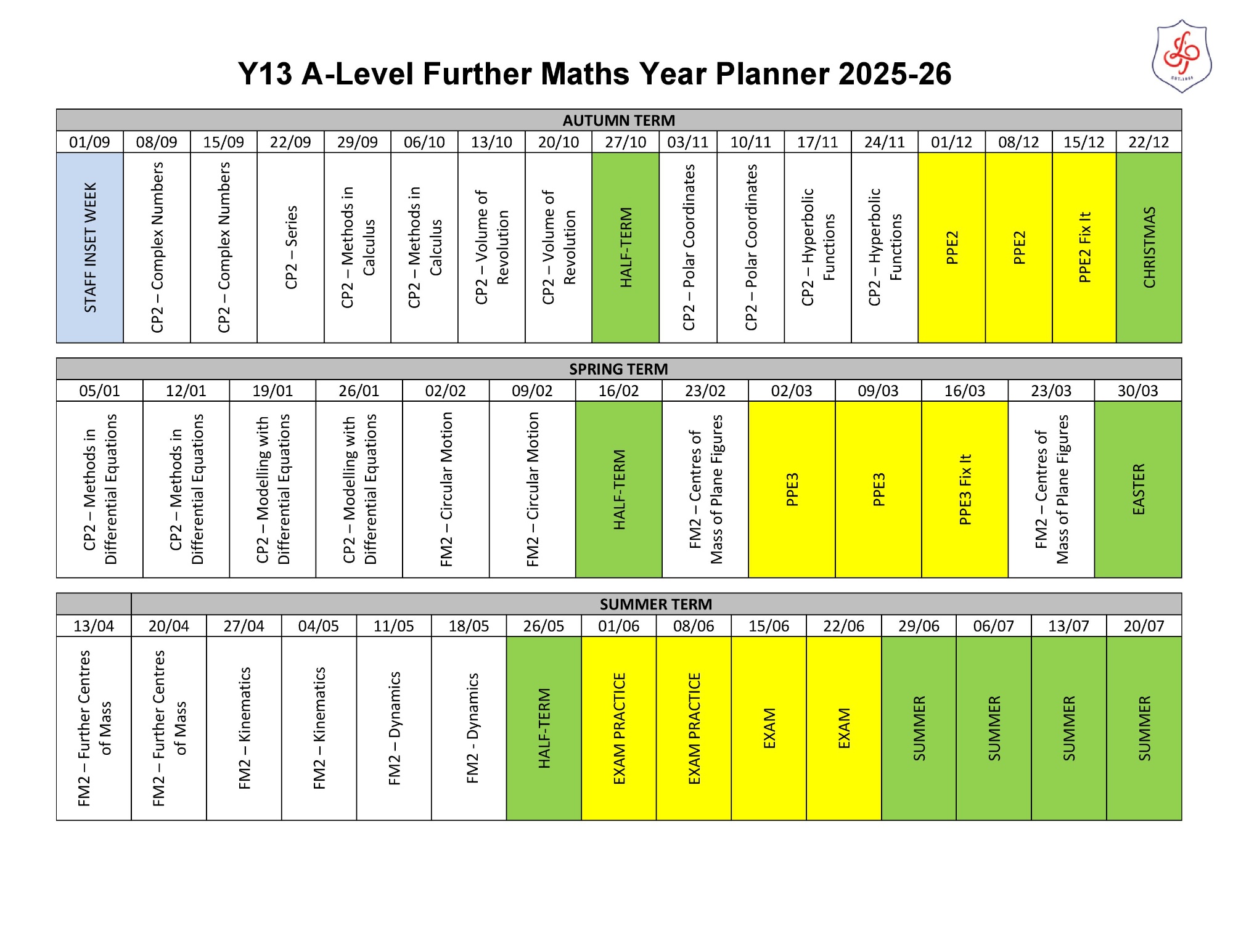
At KS5, we offer A level Mathematics, Further Mathematics, and Core Maths. A level Mathematics develops a strong understanding of pure maths, statistics and mechanics, building skills that are highly valued in higher education and employment. Further Mathematics gives our most able mathematicians the chance to study the subject at a deeper level, preparing them for competitive university courses in mathematics, physics, engineering and related fields. Core Maths is designed to support pupils who may not be taking A level Mathematics but who want to continue studying maths in a practical way, particularly useful for subjects such as Psychology, Business, Economics, and the Sciences.
Across all key stages, we emphasise the importance of STEM, helping pupils understand how mathematics connects with science, technology, engineering, the arts and design. We bring mathematics to life through real-world applications and contemporary technologies – from climate modelling and medical data analysis to robotics, digital design and architecture. Pupils are encouraged to see mathematics as more than just numbers and algebra: it is a language that explains the world, drives innovation and supports creativity.
Our goal is that pupils leave school with strong mathematical skills, the ability to think critically and solve problems, and a clear appreciation of the opportunities mathematics provides in further study, future careers and everyday life. Our passionate department of specialist teachers is dedicated to creating a supportive and challenging environment where every student can thrive.
Supporting all students across these key stages is our dedicated Maths Virtual Learning Environment (VLE). This exclusive website for LPS pupils is a comprehensive hub for KS3 and KS4, hosting direct downloads to all past exam papers, topic-specific PowerPoints, worksheets, and video tutorials. It also provides carefully selected links to the very best external maths resources, all gathered in one place. Our KS5 VLE resources are currently being expanded to provide the same exceptional level of support for our A Level and Core Maths students, further cementing its role as our central portal for maths learning and revision from Years 7 to 13.
Explore our Maths VLE here: www.sites.google.com/langdonpark.org/maths
We welcome any questions you may have about our mathematics curriculum; please feel free to contact us.
CALCULATOR: We expect every student to have a scientific calculator as part of their school equipment and to bring it to every maths lesson. It is an essential piece of equipment for learning mathematics- and two out of three of the GCSE papers students will sit require a calculator.
It MUST be a scientific calculator. The one we would recommend is the CASIO FX-85GTX. The cheapest we have found it is at Asda for £12. We would recommend marking your calculator in permanent marker with your name – we can help with this if needed.
----------------------------------------------------------------------------------------------------------------------------------------.
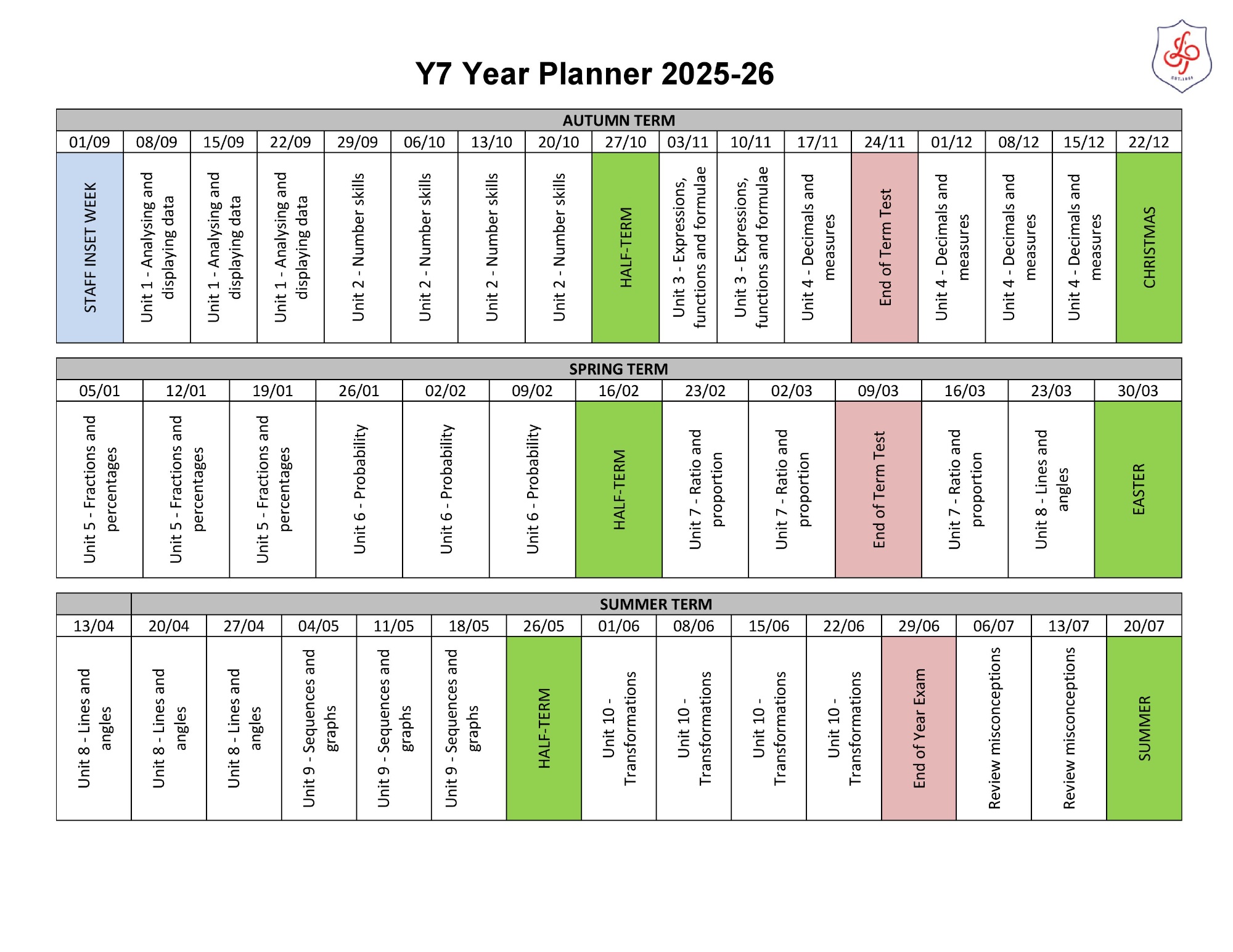
Year 7
Please click here for the Year 7 Unit Overview
Autumn term
Unit 1: Analysing and displaying data
- Mode, median and range
- Displaying data
- Grouping data
- Averages and comparing data
- Line graphs and more bar charts
Unit 2: Number skills
- Mental maths
- Addition and subtraction
- Multiplication
- Division
- Money and time
- Negative numbers
- Factors, multiples and primes
- Square numbers
Unit 3: Expressions, functions and formula
- Functions
- Simplifying expressions 1
- Simplifying expressions 2
- Writing expressions
- Substituting into formulae
- Writing formulae
Unit 4: Decimals and measures
- Decimals and rounding
- Length, mass and capacity
- Scales and measures
- Working with decimals mentally
- Working with decimals
- Perimeter
- Area
- More units of measure
Spring term
Unit 5: Fractions and percentages
- Comparing fractions
- Simplifying fractions
- Working with fractions
- Fractions and decimals
- Understanding percentages
- Percentages of amounts
Unit 6: Probability
- The language of probability
- Calculating probability
- More probability calculations
- Experimental probability
- Expected outcomes
- Direct proportion
- Writing ratios
- Using ratios
- Ratios, proportions and fractions
- Proportions and percentages
Summer term
Unit 8: Lines and angles
- Measuring and drawing angles
- Lines, angles and triangles
- Drawing triangles accurately
- Calculating angles
- Angles in a triangle
- Quadrilaterals
- Sequences
- Pattern sequences
- Coordinates and midpoints
- Extending sequences
- Straight-line graphs
- Position-to-term rules
- Congruency and enlargements
- Symmetry
- Reflection
- Rotation
- Translations and combined transformations
Year 8
Please click here for the Year 8 Unit Overview
Autumn term
Unit 1: Number
- Calculations
- Divisibility and division
- Calculating with negative integers
- Powers and roots
- Powers, roots and brackets
- More powers, multiples and factors
Unit 2: Area and volume
- Area of a triangle
- Area of a parallelogram and a trapezium
- Volume of cubes and cuboids
- 2D representations of 3D solids
- Surface area of cubes and cuboids
- Measures
Unit 3: Statistics, graphs and charts
- Pie charts
- Using tables
- Stem and leaf diagrams
- Comparing data
- Scatter graphs
- Misleading graphs
Unit 4: Expressions and equations
- Algebraic powers
- Expressions and brackets
- Factorising expressions
- One-step equations
- Two-step equations
- The balancing method
Spring term
Unit 5: Real-life graphs
- Conversion graphs
- Distance-time graphs
- Line graphs
- More line graphs
- Real-life graphs
- Curved graphs
Unit 6: Decimals and ratio
- Ordering decimals and rounding
- Place value calculations
- Calculations with decimals
- Ratio and proportion with decimals
Unit 7: Lines and angles
- Quadrilaterals
- Alternate angles and proof
- Angles in parallel lines
- Exterior and interior angles
- Solving geometric problems
Summer term
Unit 8: Calculating with fractions
- Ordering fractions
- Adding and subtracting fractions
- Multiplying fractions
- Dividing fractions
- Calculating with mixed numbers
Unit 9: Straight-line graphs
- Direct proportion on graphs
- Gradients
- Equations of straight lines
Unit 10: Percentages, decimals and fractions
- Fractions and decimals
- Equivalent proportions
- Writing percentages
- Percentages of amounts
Year 9
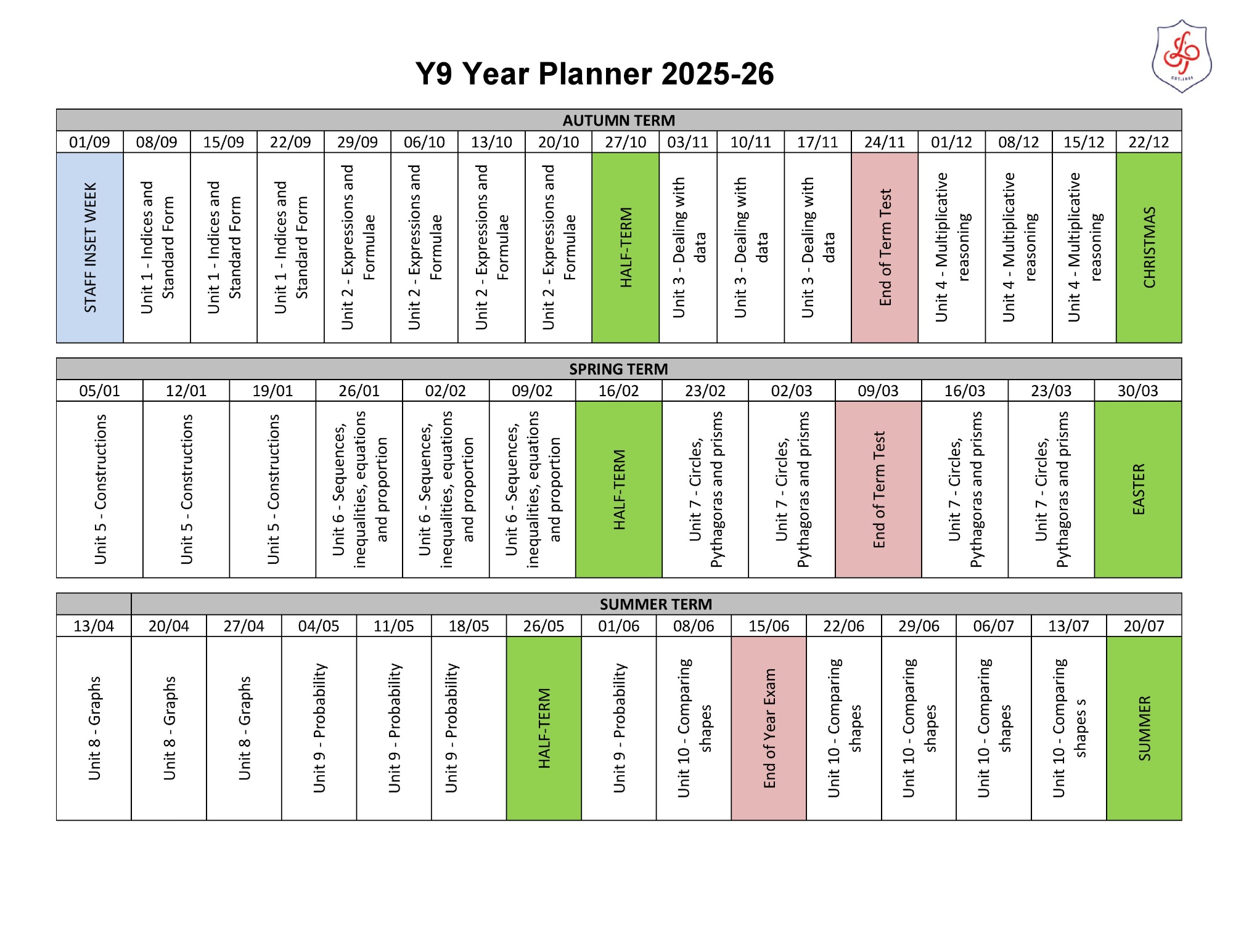
Please click here for the Year 9 Unit Overview
Autumn term
Unit 1: Indices and standard form
- Indices
- Calculations and estimates
- More indices
- Standard form
Unit 2: Expressions and formulae
- Solving equations
- Substituting into expressions
- Writing and using formulae
- Using and rearranging formulae
- Index laws and brackets
- Expanding double brackets
Unit 3: Dealing with data
- Planning a survey
- Collecting data
- Calculating averages
- Displaying and analysing data
- Presenting and comparing data
Unit 4: Multiplicative reasoning
- Enlargement
- Negative and fractional scale factors
- Percentage change
- Compound measures
- Direct and inverse proportion
Spring term
Unit 5: Constructions
- Using scales
- Basic constructions
- Constructing triangles
- Using accurate scale diagrams
Unit 6: Sequences, inequalities, equations and proportions
- nth term of arithmetic sequences
- Non-linear sequences
- Inequalities
- Solving equations
- Proportion
Unit 7: Circles, Pythagoras and prisms
- Circumference of a circle
- Area of a circle
- Pythagoras’ theorem
- Prisms and cylinders
- Errors and bounds
Summer term
Unit 8: Graphs
- Using y = mx + c
- More straight-line graphs
- Simultaneous equations
- Graphs of quadratic functions
- More non-linear graphs
Unit 9: Probability
- Mutually exclusive events
- Experimental and theoretical probability
- Sample space diagrams
- Two-way tables
- Venn diagrams
Unit 10: Comparing shapes
- Congruent and similar shapes
- Ratios in triangles
- The tangent ratio
- The sine ratio
- The cosine ratio
- Using trigonometry to find angles
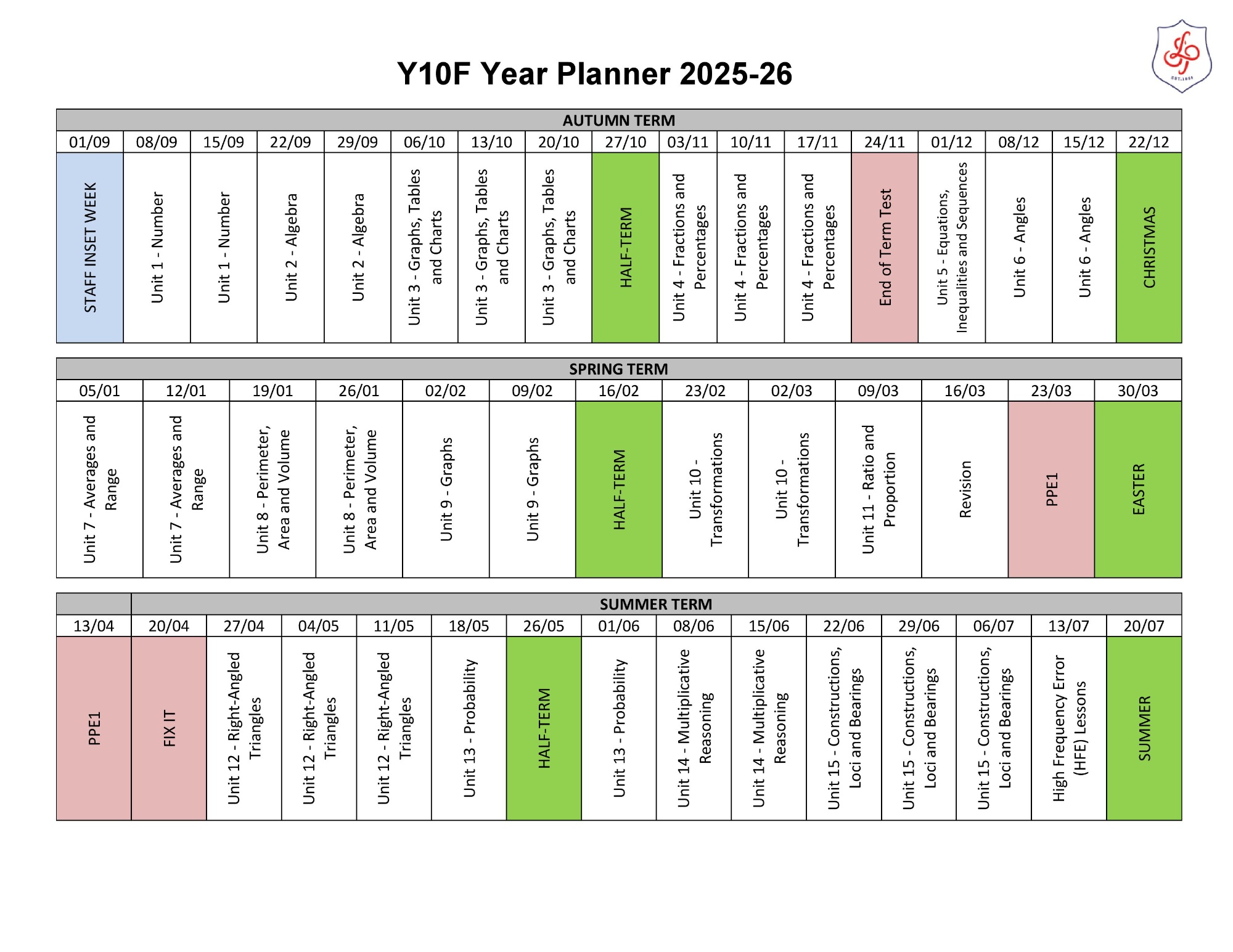
Year 10 F
Please click here for Year 10F Unit Overview
Autumn term
Unit 1: Number
- Calculations
- Decimal numbers
- Place value
- Factors and multiples
- Squares, cubes and roots
- Index notation
- Prime factors
Unit 2: Algebra
- Algebraic expressions
- Simplifying expressions
- Substitution
- Formulae
- Expanding brackets
- Factorising
- Using expressions and formulae
Unit 3: Graphs, tables and charts
- Frequency tables
- Two-way tables
- Representing data
- Time series
- Stem and leaf diagrams
- Pie charts
- Scatter graphs
- Line of best fit
Unit 4: Fractions and percentages
- Working with fractions
- Operations with fractions
- Multiplying fractions
- Dividing fractions
- Fractions and decimals
- Fractions and percentages
- Calculating percentages 1
- Calculating percentages 2
Unit 5: Equations, inequalities and sequences
- Solving equations 1
- Solving equation 2
- Solving equations with brackets
- Introducing inequalities
- More inequalities
- Using formulae
- Generating sequences
- Using the Nth term of a sequence
Spring term
Unit 6: Angles
- Properties of shapes
- Angles in parallel lines
- Angles in triangles
- Exterior and interior angles
- More exterior and interior angles
- Geometrical problems
Unit 7: Averages and range
- Mean and range
- Mode, median and range
- Types of average
- Estimating the mean
- Sampling
Unit 8: Perimeter, area and volume 1
- Rectangles, parallelograms and triangles
- Trapezia and changing units
- Area of compound shapes
- Surface area of 3D solids
- Volume of prisms
- More volume and surface area
Unit 9: Graphs
- Coordinates
- Linear graphs
- Gradient
- y = mx + c
- Real-life graphs
- Distance-time graphs
- More real-life graphs
Unit 10: Transformations
- Translations
- Reflection
- Rotation
- Enlargement
- Describing enlargements
- Combining transformations
Summer term
Unit 11: Ratio and proportion
- Writing ratios
- Using ratios 1
- Ratio and measures
- Using ratios 2
- Comparing using rations
- Using proportion
- Proportion and graphs
- Proportion problems
Unit 12: Right-angled trigonometry
- Pythagoras' theorem 1
- Pythagoras' theorem 2
- Trigonometry: the sine ratio 1
- Trigonometry: the sine ratio 2
- Trigonometry: the cosine ratio
- Trigonometry: the tangent ratio
- Finding lengths and angles using trigonometry
Unit 13: Probability
- Calculating probability
- Two events
- Experimental probability
- Venn diagram
- Tree diagrams
- More tree diagrams
Unit 14: Multiplicative reasoning
- Percentages
- Growth and decay
- Compound measures
- Distance, speed and time
- Direct and inverse proportion
Unit 15: Constructions, loci and bearings
- 3D Solids
- Plan and elevations
- Accurate drawings 1
- Scale drawing and maps
- Accurate drawings 2
- Constructions
- Loci and regions
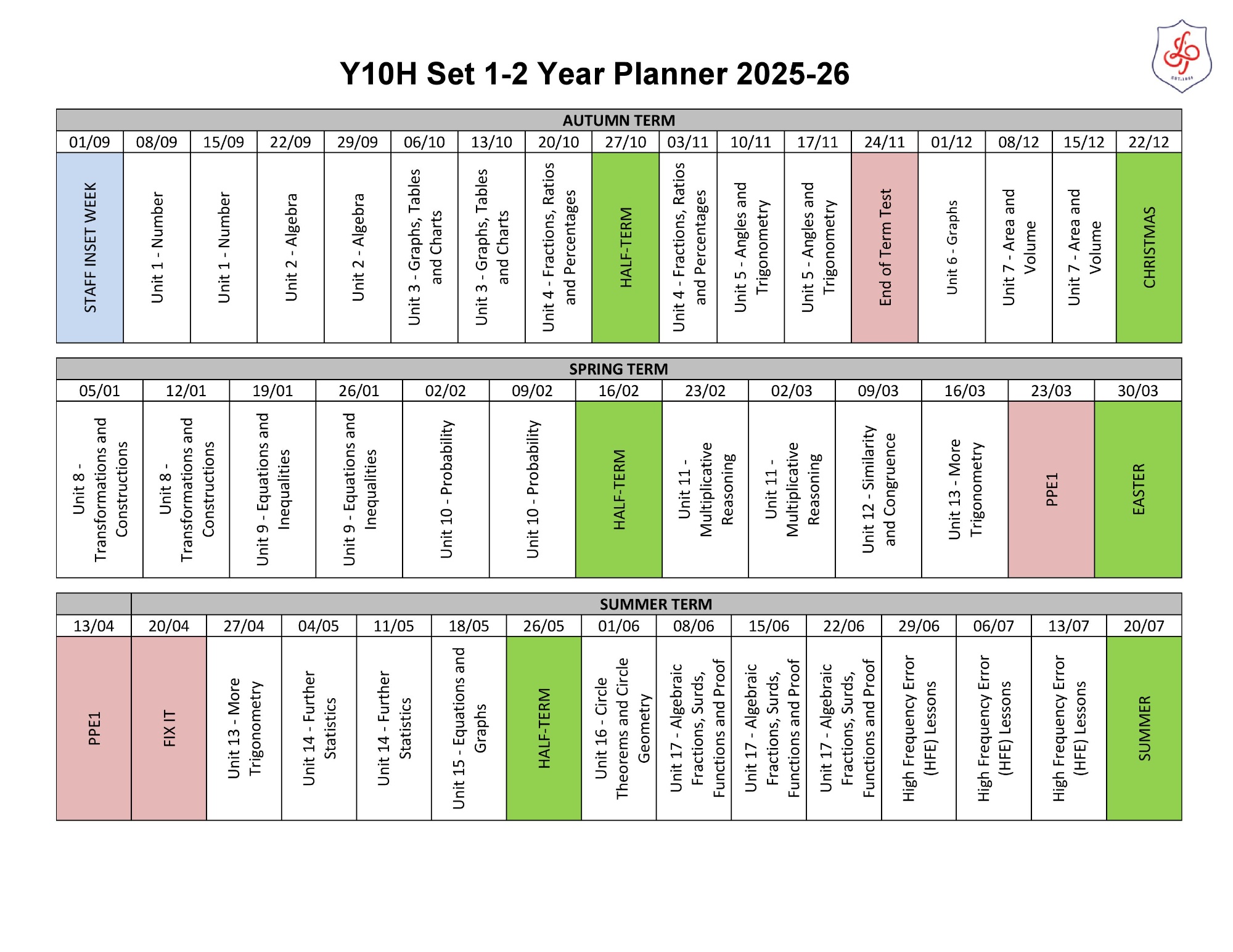
Year 10 H
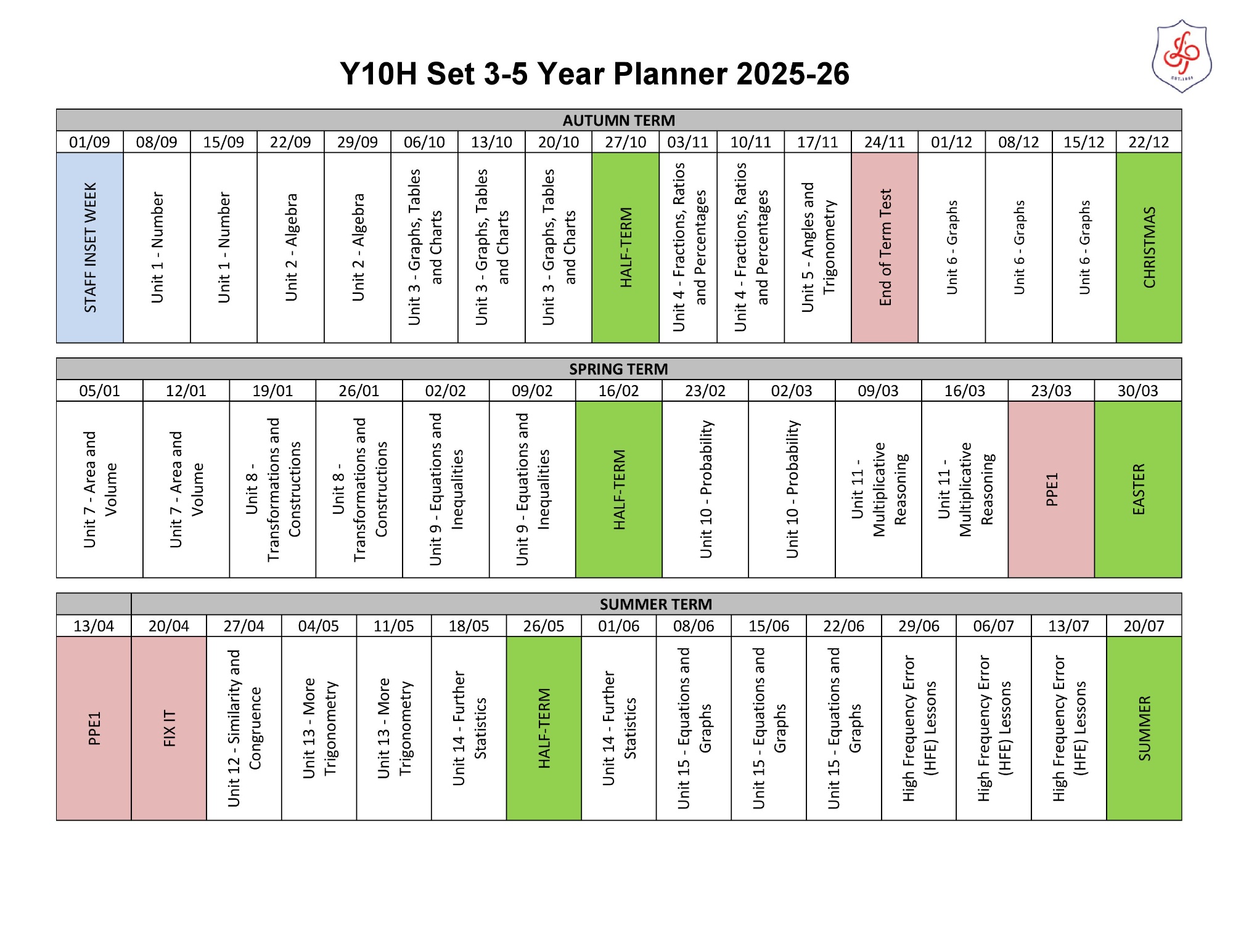Please click here to see the Year 10H Unit Overview
Autumn term
Unit 1: Number
- Number problems and reasoning
- Place value and estimating
- HCF and LCM
- Calculating with powers (indices)
- Zero, negative and fractional indices
- Powers of 10 and standard form
- Surds
Unit 2: Algebra
- Algebraic indices
- Expanding and factorising
- Equations
- Formulae
- Linear sequences
- Non-linear sequences
- More expanding and factorising
Unit 3: Interpreting and representing data
- Statistical diagrams 1
- Time series
- Scatter graphs
- Line of best fit
- Averages and range
- Statistical diagrams 2
Unit 4: Fractions, ratio and percentages
- Fractions
- Ratios
- Ratio and proportion
- Percentages
- Fractions, decimals and percentage
Unit 5: Angles and trigonometry
- Angle properties of triangles and quadrilaterals
- Interior angles of a polygon
- Exterior angles of a polygon
- Pythagoras' theorem 1
- Pythagoras' theorem 2
- Trigonometry 1
- Trigonometry 2
Spring term
Unit 6: Graphs
- Linear graphs
- More linear graphs
- Graphing rates of change
- Real-life graphs
- Line segments
- Quadratic graphs
- Cubic and reciprocal graphs
- More graphs
Unit 7: Area and volume
- Perimeter and area
- Units and accuracy
- Prisms
- Circles
- Sectors of circles
- Cylinders and spheres
- Pyramids and cones
Unit 8: Transformations and constructions
- 3D solids
- Reflection and rotation
- Enlargement
- Translations and combinations of different transformations
- Scale drawings and bearings
- Constructions 1
- Constructions 2
- Loci
Unit 9: Equations and inequalities
- Solving linear inequalities
- Solving quadratic equations 1
- Solving quadratic equations 2
- Completing the square
- Solving simple simultaneous equations
- More simultaneous equations
- Solving linear and quadratic simultaneous equations
Unit 10: Probability
- Combined events
- Mutually exclusive events
- Experimental probability
- Independent events and tree diagrams
- Conditional probability
- Venn diagrams and set notation
Summer term
Unit 11: Multiplicative reasoning
- Growth and decay
- Compound measures
- More compound measures
- Ratio and proportions
Unit 12: Similarity and congruence
- Congruence
- Geometric proof and congruence
- Similarity
- More similarity
- Similarity in 3D solids
Unit 13: More trigonometry
- Accuracy
- Graph of the sine function
- Graph of the cosine function
- Graph of the tangent function
- Calculating area and the sine rule
- The cosine rule and 2D trigonometric problems
- Solving problems in 3D
- Transforming trigonometric graphs 1
- Transforming trigonometric graphs 2
Unit 14: Further statistics
- Sampling
- Cumulative frequency
- Box plots
- Drawing histograms
- Interpreting histograms
- Comparing and describing distributions
Unit 15: Equations and graphs
- Solving simultaneous equations graphically
- Representing inequalities graphically
- Quadratic equations
- Using quadratic graphs
- Cubic equations
- Using iteration to solve equations
Year 11 F
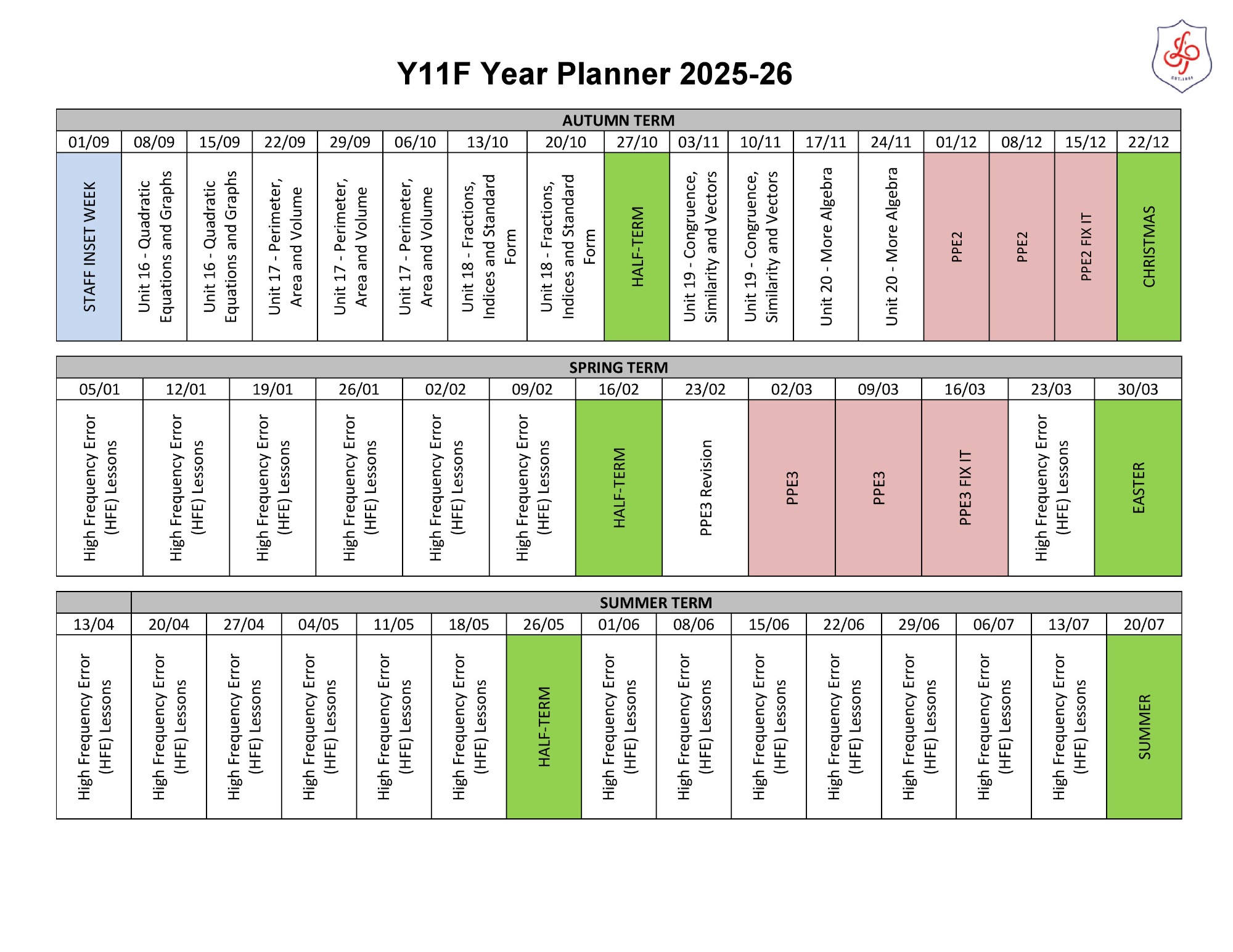
Please click here to see the Year 11 F Unit Overview
Autumn term
Unit 16: Quadratic equations and graphs
- Prior knowledge check
- Expanding double brackets
- Plotting quadratic graphs
- Using quadratic graphs
- Factorising quadratic expressions
- Solving quadratic equations algebraically
Unit 17: Perimeter, area and volume 2
- Circumference of a circle 1
- Circumference of a circle 2
- Area of a circle
- Semicircles and sectors
- Composite 2D shapes and cylinders
- Pyramids and cones
- Spheres and composite solids
Unit 18: Fractions, indices and standard form
- Multiplying and dividing fractions
- The laws of indices
- Writing large numbers in standard form
- Writing small numbers in standard form
- Calculating with standard form
Unit 19: Congruence, similarity and vectors
- Similarity and enlargement
- More similarity
- Using similarity
- Congruence 1
- Congruence 2
- Vectors 1
- Vectors 2
Unit 20: More algebra
- Graphs of cubic and reciprocal functions
- Non-linear graphs
- Solving simultaneous equations graphically
- Solving simultaneous equations algebraically
- Rearranging formulae
- Proof
Spring term
- Exam practice
- High frequency topics
- High frequency error topics
Summer term
- Exam practice
- High frequency topics
- High frequency error topics
Year 11 H
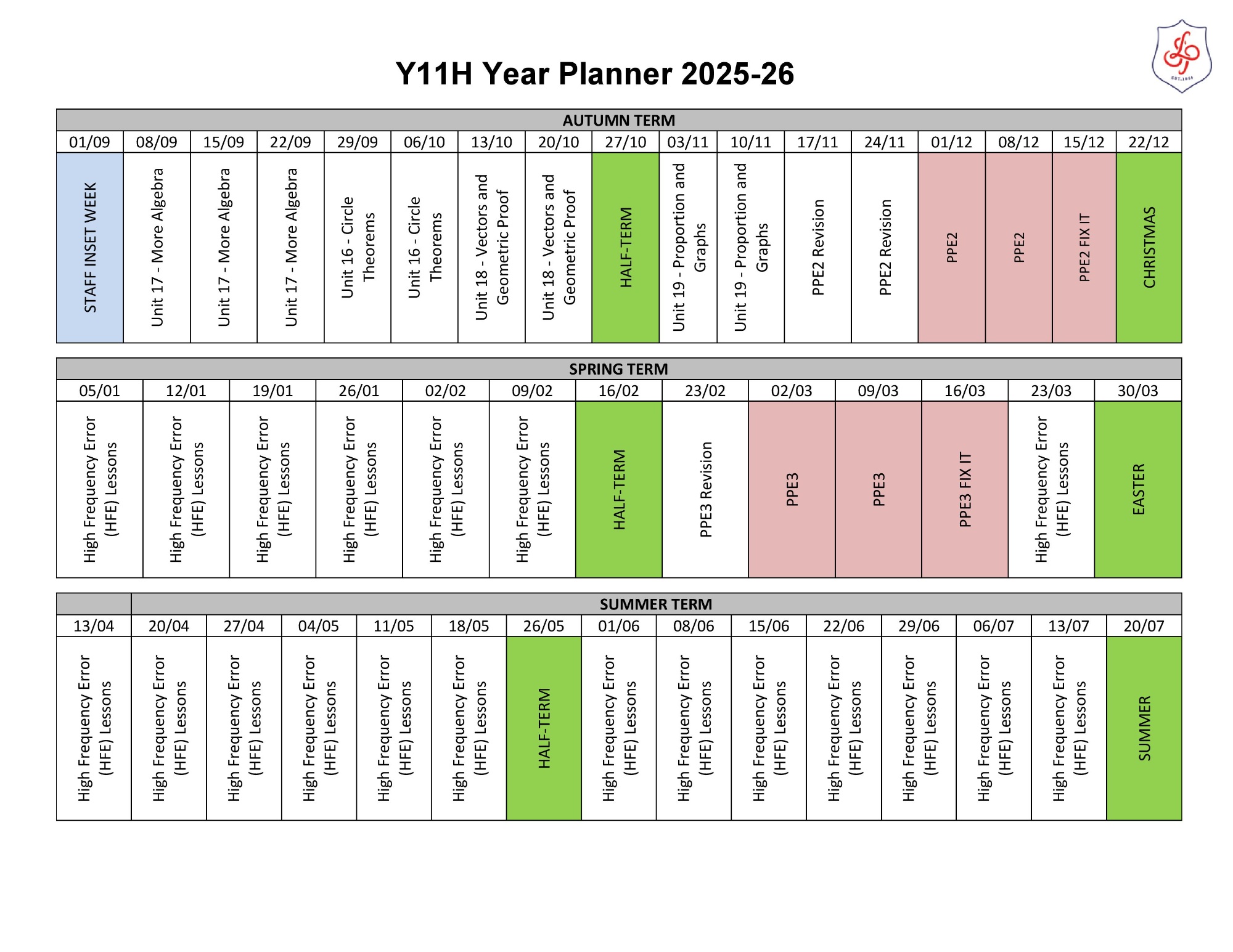
Please click here to see the Year 11 H Unit Overview
Autumn term
Unit 16: Circle theorems
- Radii and chords
- Tangents
- Angles in circles 1
- Angles in circles 2
- Applying circle theorems
Unit 17: More algebra
- Rearranging formulae
- Algebraic fractions
- Simplifying algebraic fractions
- More algebraic fractions
- Proof
- Surds
- Solving algebraic fraction equations
- Functions
Unit 18: Vectors and geometric proofs
- Vectors and vector notation
- Vector arithmetic
- More vector arithmetic
- Parallel vectors and collinear points
- Solving geometric problems
Unit 19: Proportions and graphs
- Direct proportion
- More direct proportion
- Inverse proportion
- Exponential functions
- Non-linear graphs
- Translating graphs of functions
- Reflecting graphs of functions
Spring term
- Exam practice
- High frequency topics
- High frequency error topics
Summer term
- Exam practice
- High frequency topics
- High frequency error topics
A Level Maths
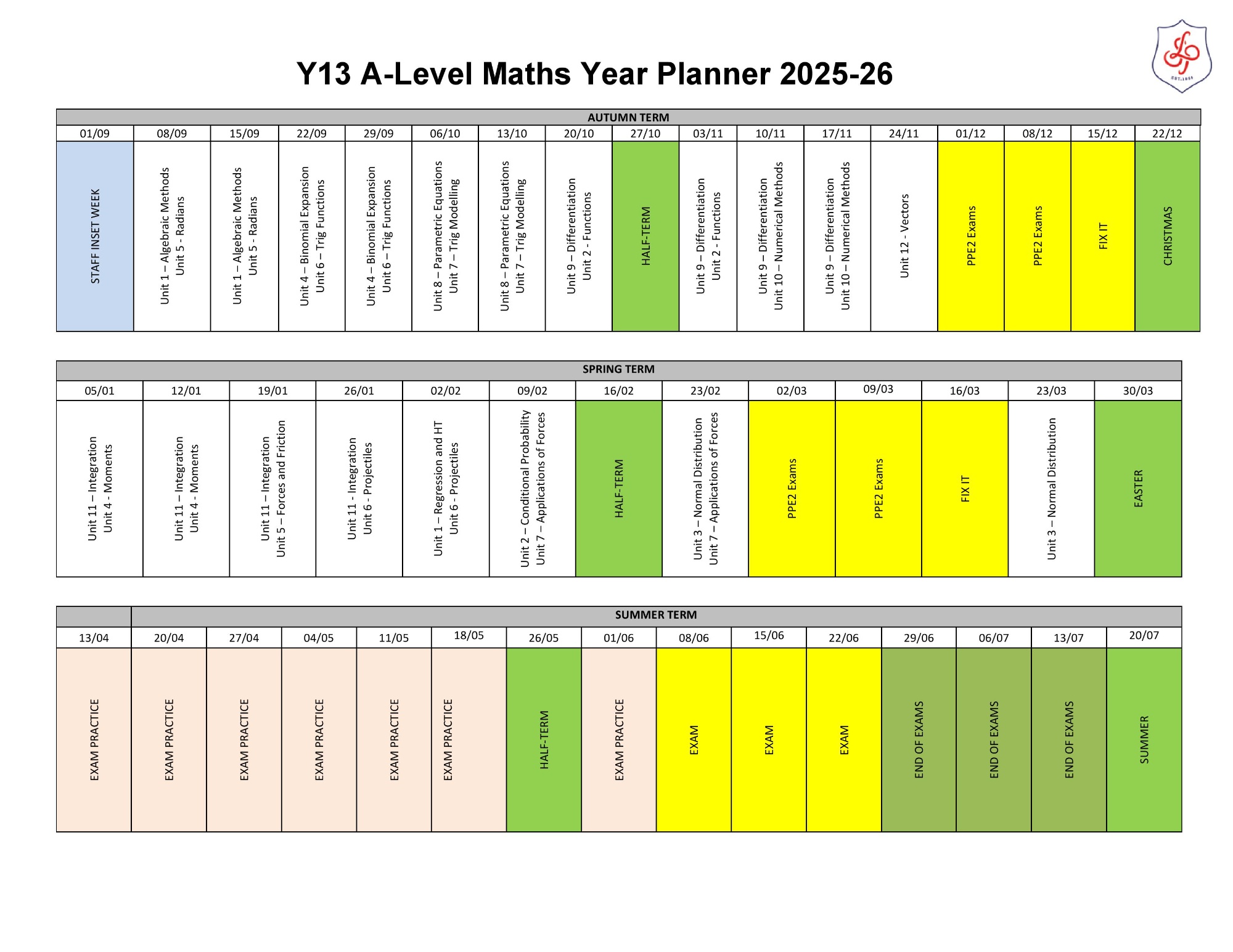
Pure Mathematics
- Proof
- Mathematical proof (deduction, exhaustion, counter-example, contradiction)
Algebra and Functions
- Laws of indices
- Manipulation of surds
- Quadratic functions and equations
- Simultaneous equations
- Linear and quadratic inequalities
- Polynomial algebra
- Rational expressions
- Graphs of functions
- Transformations of functions
- Composite and inverse functions
- Decomposition into partial fractions
Coordinate Geometry
- Equation of a straight line
- Circle geometry
- Parametric equations and conversion
- Application of parametric equations
Sequences and Series
- Binomial expansion
- Arithmetic and geometric sequences and series
- Sigma notation
- Use of sequences and series in modelling
Trigonometry
- Definitions of sine, cosine, and tangent
- Radian measure
- Small angle approximations
- Sine, cosine, and tangent functions and their graphs
- Secant, cosecant, cotangent, and inverse trigonometric functions
- Trigonometric identities and equations
- Double angle and addition formulas
- Applications in context
Exponentials and Logarithms
- Exponential functions and their graphs
- Logarithmic functions and their properties
- Laws of logarithms
- Exponential growth and decay models
Differentiation
- Derivatives and their interpretation as rates of change
- Differentiation of standard functions
- Higher-order derivatives
- Tangents, normals, and stationary points
- Differentiation techniques (product, quotient, chain rule)
- Implicit and parametric differentiation
- Applications in various contexts
Integration
- Fundamental theorem of calculus
- Integration of standard functions
- Definite and indefinite integrals
- Integration techniques (substitution, by parts, using partial fractions)
- Applications to areas under curves and solving differential equations
Numerical Methods
- Root finding using change of sign methods
- Iterative methods and their convergence
- Newton-Raphson method
- Numerical integration (trapezium rule)
Vectors
- Vectors in 2D and 3D
- Magnitude and direction of vectors
- Vector operations (addition, scalar multiplication)
- Position vectors and distance between points
- Applications in various contexts
Statistics
- Statistical Sampling
- Population and sample concepts
- Sampling techniques and critique
- Data Presentation and Interpretation
- Interpretation of data diagrams
- Scatter diagrams and regression
- Measures of central tendency and variation
- Outliers and data cleaning
Probability
- Mutually exclusive and independent events
- Conditional probability
Statistical Distributions
- Discrete probability distributions
- Binomial and normal distributions
Statistical Hypothesis Testing
- Language and concepts of hypothesis testing
- Testing proportions and means
- Correlation coefficients and their interpretation
Mechanics
- Quantities and Units in Mechanics
- Use of SI units and derived units
Kinematics
- Constant acceleration (suvat equations)
- Motion in a straight line
- Velocity-time and displacement-time graphs
Forces and Newton’s Laws
- Forces and equilibrium
- Newton’s laws of motion
- Application of Newton’s laws
Moments
- Moment of a force and its application
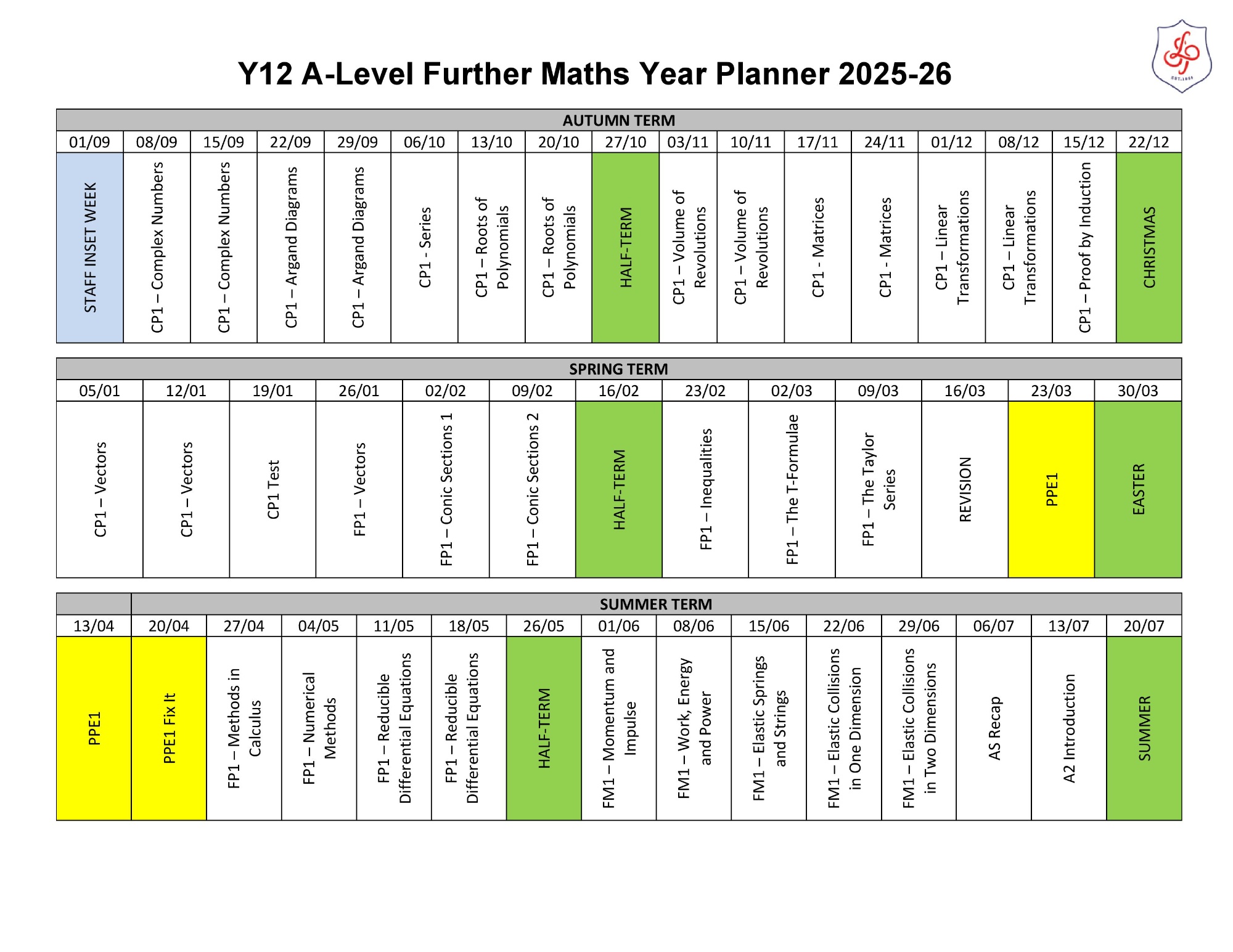
Further Maths
Core content (compulsory)
Overarching Themes
- OT1: Mathematical argument, language, and proof
- OT2: Mathematical problem-solving
- OT3: Mathematical modelling
Compulsory content areas
A: Proof
- B: Complex Numbers
- C: Matrices
- D: Further Algebra and Functions
- E: Further Calculus
- F: Further Vectors
- G: Polar Coordinates
- H: Hyperbolic Functions
- I: Differential Equations
- J: Numerical Method
Mechanics
- MA: Dimensional Analysis
- MB: Momentum and Collisions
- MC: Work, Energy, and Power
- MD: Circular Motion
- ME: Centres of Mass and Moments
Statistics
- SA: Discrete Random Variables (DRVs) and Expectation
- SB: Poisson Distribution
- SC: Type I and Type II Errors
- SD: Continuous Random Variables (CRVs)
- SE: Chi-Squared Tests for Association
- SF: Exponential Distribution
- SG: Inference – One Sample t-distribution
- SH: Confidence Intervals
Discrete Mathematics
- DA: Graphs
- DB: Networks
- DC: Network Flows
- DD: Linear Programming
- DE: Critical Path Analysis
- DF: Game Theory for Zero-Sum Games
- DG: Binary Operations
Level 2 Core Maths
Application of statistics
- Infer properties of populations or distributions from a sample
- Interpret and construct tables and line graphs for time series data
- Construct and interpret diagrams for grouped discrete data and continuous data
- Interpret, analyse, and compare distributions of data sets using graphical representations
- Recognise and interpret measures of central tendency, variance, and standard deviation
- Recognise correlation and understand its limitations
- Apply and interpret explanatory (independent) and response (dependent) variables
- Draw estimated lines of best fit, make predictions, and understand the product moment correlation coefficient
- Use and interpret linear regression
- Use and interpret Spearman’s rank correlation coefficient
Probability
- Understand empirical unbiased samples and their relation to theoretical probability distributions
- Systematically enumerate sets and combinations of sets using tree diagrams
- Calculate the probability of independent and dependent combined events using various representations
- Calculate and interpret conditional probabilities
- Understand and interpret probability notation, including Venn diagrams and laws of probability
- Interpret risk and apply it to real-life contexts such as finance, insurance, and trading
Linear programming
- Translate situations or procedures into algebraic expressions or formulae
- Plot and interpret graphs of linear functions
- Solve linear equations and inequalities in one or two variables
- Formulate and solve linear programming problems with up to three variables
- Interpret solutions graphically, including using ruler and vertex methods
- Consider integer solutions in linear programming problems
Sequences and growth
- Solve and interpret growth and decay problems, including compound interest
- Calculate simple and compound interest
- Recognise and interpret graphs of various functions (quadratic, reciprocal, polynomial, exponential)
- Interpret gradients as rates of change and apply these concepts numerically and graphically
- Calculate with roots and indices
- Recognise and use arithmetic and geometric sequences and series
- Understand and apply sigma notation